We meet again in my learning notes.

“Make my learning sticks more, and solidify my understandce..” – understandce, that should be a word.

Today I’m publishing notes about Heap. This one gonna be a long note.

What is Heap?

Heaps are trees with some extras.

TL;DR: Heap is a specialized tree structure with some rules that designed for efficient retrieval of the maximum or minimum element.

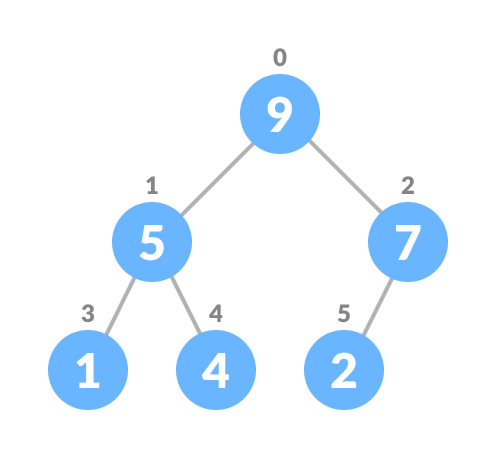
Before we go further, we gotta know some tree characteristics that are related to Heaps, which are Complete Tree and Perfect Tree.

A Complete Tree: is one in which all levels, except possibly the last, are fully filled, and all nodes are as left as possible.

A Perfect Binary Tree is a tree in which all interior nodes have two children, and all leaf nodes are at the same level.

Heap is an almost complete binary (or n-ary) tree, meaning it follows the characteristics of a complete tree but allows for a slight relaxation in terms of completeness. However, it is not a Perfect binary tree, indicating that it doesn’t strictly adhere to the perfect tree structure, allowing for some variability in the number of children each node may have.

Why it’s named Heaps?

The name “Heap” probably comes from how elements are stacked, much like creating a pile of things.

In a Heap, the item we like the most (or the least, depending on the type of Heap) is always at the top, making it easy to grab or remove

Max Heap vs Min Heap?

We’re going to talk about this from the general perspective, there are basically two most common kinds of heaps:

Max Heap: In a Max Heap, the value of each node is greater than or equal to the values of its children. The maximum value in the heap is always at the root.

Min Heap: In a Min Heap, the value of each node is less than or equal to the values of its children. The minimum value in the heap is always at the root.

How Are The Rules/Property of Heaps?

So here are the basic propertiers or rules that must be maintained in a heap:

• Ordering Rule: In a Max Heap, every parent node has a value greater than or equal to its children; in a Min Heap, every parent node has a value less than or equal to its children.
• Complete Binary Tree: The tree is almost complete, with all levels, except possibly the last, fully filled, and all nodes placed as left as possible.

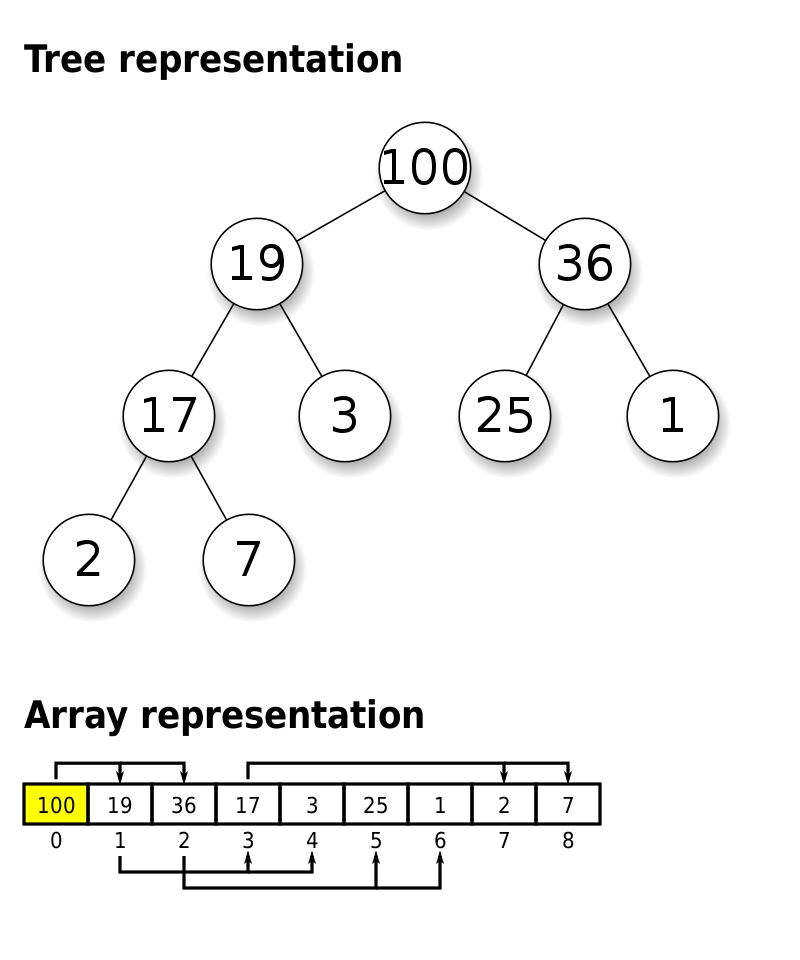
Binary Heaps especially can be represented as a simple array like these:

# Simple representation of a binary heap using an array
heap = [5, 3, 8, 1, 7, 6]

# Indexing and Relationships:
# Parent(i) = i // 2
# Left Child(i) = 2 * i
# Right Child(i) = 2 * i + 1

In this array representation, if the element is at index i, its left child will be at index 2 * i and the right child at index 2 * i + 1. The parent of an element at index i will be at index i // 2.

But if the rules are so, something will be triggered on insert and mutations right? How?

Yes, there is a thing we will call ‘HEAPIFY’ that essentially will rearrange remaining elements upon a plucking on its element.

# Unified Heapify Function
def heapify(heap, index, heap_size):
    largest = index
    left_child = 2 * index + 1
    right_child = 2 * index + 2

    # Find the largest among the node and its children
    if left_child < heap_size and heap[left_child] > heap[largest]:
        largest = left_child
    if right_child < heap_size and heap[right_child] > heap[largest]:
        largest = right_child

    # Swap if necessary and recursively call heapify
    if largest != index:
        heap[index], heap[largest] = heap[largest], heap[index]
        heapify(heap, largest, heap_size)

# Insertion with Heapify
def insert(heap, value):
    heap.append(value)
    current_index = len(heap) - 1
    
    while current_index > 0:
        parent_index = (current_index - 1) // 2
        if heap[current_index] > heap[parent_index]:
            heap[current_index], heap[parent_index] = heap[parent_index], heap[current_index]
            current_index = parent_index
        else:
            break

# Deletion with Heapify
def delete(heap):
    if not heap:
        return None

    heap[0], heap[-1] = heap[-1], heap[0]
    deleted_value = heap.pop()
    heapify(heap, 0, len(heap))

    return deleted_value

When an element is inserted, or a deletion occurs, the heap rules are maintained through a process called “Heapify Up” for insertion and “Heapify Down” for deletion. These processes ensure that the heap properties are preserved after the modification.

Closing Word for Part I

This post turned out to be a bit longer. So I decided to put it into two parts.

For now so far, in summary, Heaps are cool. Haha. Really, there are many things that I learnt when researching about this data structure. In next part I will explaining why this data structure is cool.

See you in part two~